12. 反向传播
梯度下降解决方案
def gradient_descent_update(x, gradx, learning_rate):
"""
Performs a gradient descent update.
"""
x = x - learning_rate * gradx
# Return the new value for x
return x我们调整了旧的 x,朝着 gradx 的方向推动,推力为 learning_rate。减去 learning_rate * gradx。注意,梯度一开始朝着最陡上升方向,所以将 x 减去 learning_rate * gradx 使其变成最陡下降方向。你可以通过将减法替换为加法自己进行确定。
梯度和反向传播
我们现在知道如何使用梯度更新我们的权重和偏置,我们还需要知道如何计算所有节点的梯度。对于每个节点,我们需要根据梯度更改代价的值(考虑到该节点的值)。这样,我们做出的梯度下降更新最终会实现最低代价。
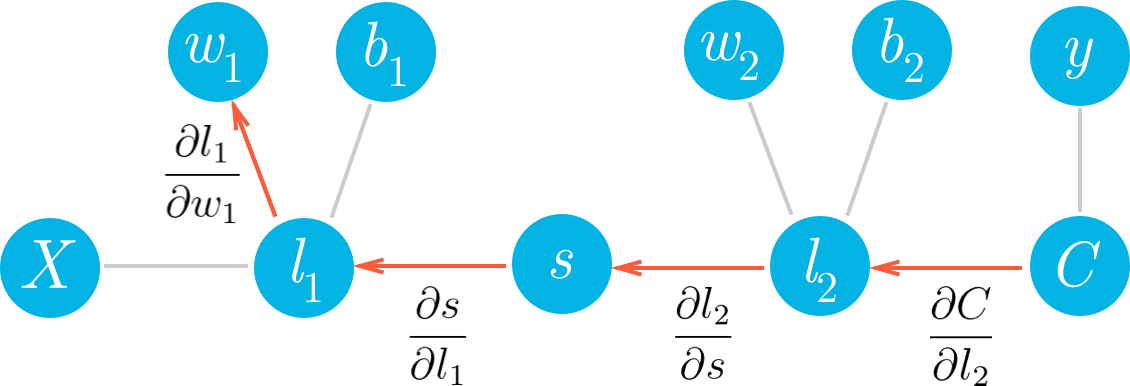
我们来看一个网络,其中具有一个线性节点 l_1,一个 S 型节点 s,以及另一个线性节点 l_2,还有一个 MSE 节点,用于计算代价 C。
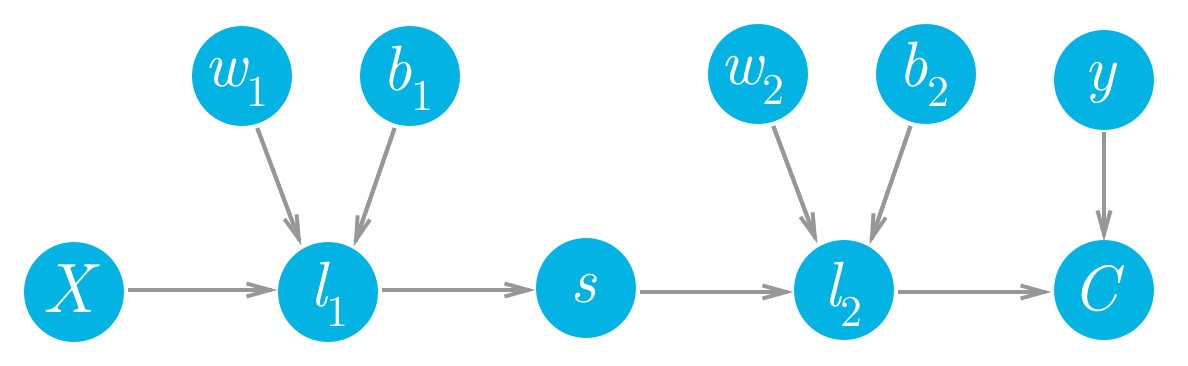
简单的两层网络的前向传递。
用 MiniFlow 编写的话,应该如下所示:
X, y = Input(), Input()
W1, b1 = Input(), Input()
W2, b2 = Input(), Input()
l1 = Linear(X, W1, b1)
s = Sigmoid(l1)
l2 = Linear(s, W2, b2)
cost = MSE(l2, y)我们可以看到这些节点的每个值都向前流动,最终生成代价 C。例如,第二个线性节点 l_2 的值进入代价节点并确定该节点的值。更改 l_2 将导致 C 相应地出现更改。我们可以将更改之间的这种关系写成梯度。
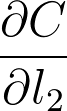
这就是梯度的含义,是一种斜率,表示给出 l_2 中的更改,你会对代价 \partial C 进行多大幅度的更改。所以,节点的代价梯度更大的话,代价就会改变更大。这样,我们可以对每个节点的代价带来的影响进行分配。节点的梯度越大,就会对最终的代价影响越大。节点的影响越大,我们就会在梯度下降步骤中更新幅度越大。
如果我们想更新某个梯度下降的权重,我们需要知道这些权重对应的代价的梯度。看看我们可以如何使用此框架算出第二层权重 w_2 的梯度。我们想要计算 C 相对于 w_2 的梯度:
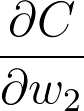
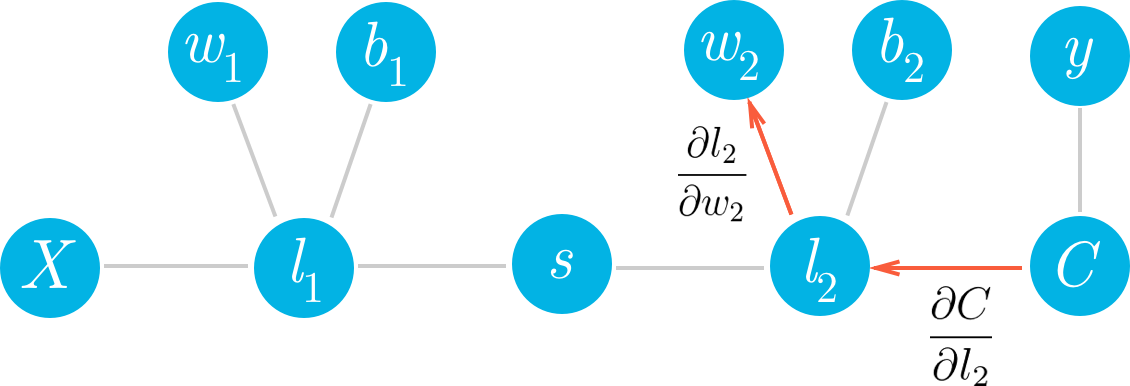
我们可以从图表中看出,w_2 与 l_2 相关联,所以更改 w_2 将导致 l_2 出现更改,从而导致 C 出现更改。我们可以通过在网络中将代价梯度发送回去,将影响分配给 w_2。首先,你知道 l_2 对 C 的影响有多大,然后知道 w_2 对 l_2 的影响有多大。将这些梯度相乘可以得出归为 w_2 的总影响。
先修条件
下面我们将介绍反向传播的数学原理,你需要掌握多元微积分知识。如果你需要复习下这方面的知识,强烈建议你查看以下资源:
- 可汗学院关于偏导数的课程
- 另一个关于梯度的视频
- 最后,如何使用链式法则
继续
将这些梯度相乘只是链式法则的一种应用:
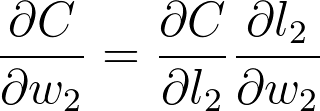
可以从图表中看出,w_2、l_2 和 C 相互链接在一起。如果 w_2 发生任何更改,将导致 l_2 出现更改,更改幅度由梯度 \partial l_2 / \partial w_2 决定。因为 l_2 更改了,这将导致代价 C 出现更改,更改幅度由梯度 \partial C / \partial l_2 决定。你可以将链式法则看做多米诺效应,网络中的某项更改将从网络中传播开来,并一路更改其他节点。
如果你将链式法则看做普通的分数,可以看到分母上的 \partial l_2 和分子消掉了,获得 \partial C / \partial w_2(虽然和普通分子的计算过程并不完全一样,但是可以帮助你理解)。现在来算算 w_2 的梯度。首先,我们需要知道 l_2 的梯度。
提醒下,代价是:
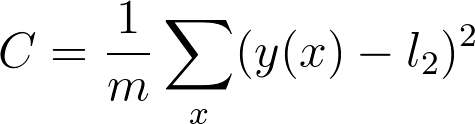
第二个线性节点的值为
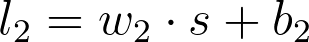
w_2、 s 和 b_2 都是向量,w_2 \cdot s 表示 w_2 和 s 的点积。
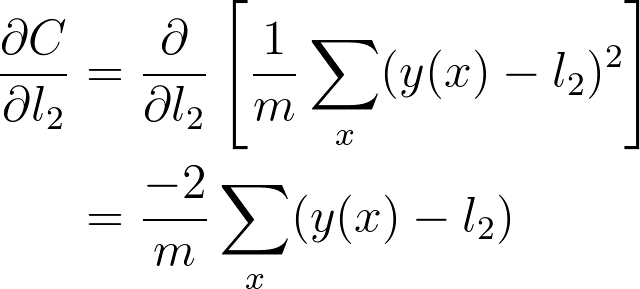
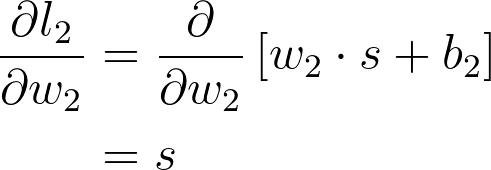
将这些放一起,可以得出 w_2 的梯度
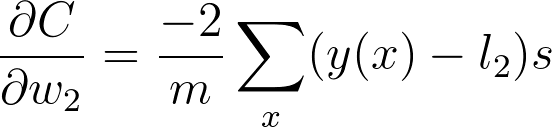
这是你在 w_2 的梯度下降更新中用到的梯度。可以看出,我们在图表上一直往回计算,将一路上发现的所有梯度相乘。
现在,我们再深入一步,计算 w_1 的梯度。和之前用到的方法一样,在图表上一直往回计算。
希望现在你能明白如何通过查看图表写出 w_1 的梯度。我们将使用链式法则在图表上一直往回计算,得出每个节点的梯度,直到算出 w_1 的梯度。
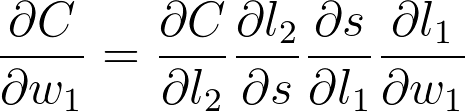
现在我们可以计算此表达式中的每个梯度,以便得出 w_1 的梯度
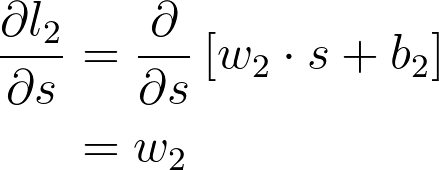
下一步是 S 型函数 s = f(l_1) 的梯度。因为这里使用的是逻辑函数,所以导数可以写成 S 型函数本身
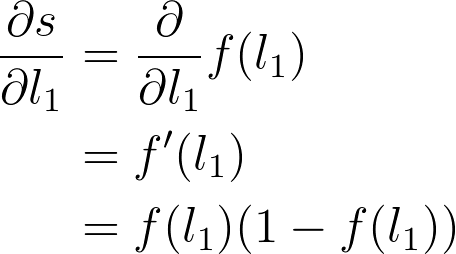
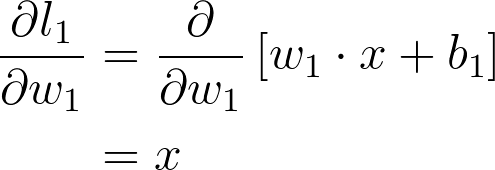
将所有这一切放在一起,得出
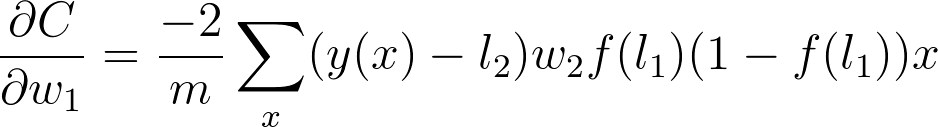
现在可以看到清晰的规律了。要算出梯度,只需将它前面所有节点(从代价那开始)的梯度相乘。这就是反向传播概念。梯度在网络上向后传播,并使用梯度下降来更新权重和偏置。如果某个节点具有多个向外的节点,则直接将每个节点的梯度相加即可。
在 MiniFlow 中实现
我们来看看如何在 MiniFlow 中实现这一流程。在图表中可以看到每个节点从传出节点那获得代价梯度。例如,节点 l_1 通过 S 型节点 s 获取 \partial C / \partial l_1。然后,l_1 将代价梯度继续传递给权重节点 w_1,但是会乘以 \partial l_1 / \partial w_1,即 l_1 的梯度除以其输入 w_1。
所以,每个节点会将代价梯度传递给传入节点,每个节点将从其传出节点那获得代价梯度。然后,对于每个节点,我们需要算出一个梯度,即代价梯度乘以该节点的梯度除以其输出。下面我为 Linear 节点写出了这一流程。
# Initialize a partial for each of the inbound_nodes.
self.gradients = {n: np.zeros_like(n.value) for n in self.inbound_nodes}
# Cycle through the outputs. The gradient will change depending
# on each output, so the gradients are summed over all outputs.
for n in self.outbound_nodes:
# Get the partial of the cost with respect to this node.
grad_cost = n.gradients[self]
# Set the partial of the loss with respect to this node's inputs.
self.gradients[self.inbound_nodes[0]] += np.dot(grad_cost, self.inbound_nodes[1].value.T)
# Set the partial of the loss with respect to this node's weights.
self.gradients[self.inbound_nodes[1]] += np.dot(self.inbound_nodes[0].value.T, grad_cost)
# Set the partial of the loss with respect to this node's bias.
self.gradients[self.inbound_nodes[2]] += np.sum(grad_cost, axis=0, keepdims=False)新的代码
自上次查看 MiniFlow 起,MiniFlow 已经出现了几处更改:
首先是 Node 类现在具有一个 backward 方法,并且添加了新的属性 self.gradients,用于在反向传递过程中存储和缓存梯度。
class Node(object):
"""
Base class for nodes in the network.
Arguments:
`inbound_nodes`: A list of nodes with edges into this node.
"""
def __init__(self, inbound_nodes=[]):
"""
Node's constructor (runs when the object is instantiated). Sets
properties that all nodes need.
"""
# A list of nodes with edges into this node.
self.inbound_nodes = inbound_nodes
# The eventual value of this node. Set by running
# the forward() method.
self.value = None
# A list of nodes that this node outputs to.
self.outbound_nodes = []
# New property! Keys are the inputs to this node and
# their values are the partials of this node with
# respect to that input.
self.gradients = {}
# Sets this node as an outbound node for all of
# this node's inputs.
for node in inbound_nodes:
node.outbound_nodes.append(self)
def forward(self):
"""
Every node that uses this class as a base class will
need to define its own `forward` method.
"""
raise NotImplementedError
def backward(self):
"""
Every node that uses this class as a base class will
need to define its own `backward` method.
"""
raise NotImplementedError第二项更改是辅助函数 forward_pass()。该函数被替换成了 forward_and_backward()。
def forward_and_backward(graph):
"""
Performs a forward pass and a backward pass through a list of sorted nodes.
Arguments:
`graph`: The result of calling `topological_sort`.
"""
# Forward pass
for n in graph:
n.forward()
# Backward pass
# see: https://docs.python.org/2.3/whatsnew/section-slices.html
for n in graph[::-1]:
n.backward()设置
下面是 sigmoid 函数 w.r.t 的导数 x:
sigmoid(x) = 1 / (1 + exp(-x))
\frac {\partial sigmoid}{\partial x} = sigmoid(x) * (1 - sigmoid(x))
- 通过完成
miniflow.py中的backward方法,完成对Sigmoid节点的反向传播实现。 - 其他所有节点的
backward方法已经实现。看看这些实现可能有所帮助。
Start Quiz: